Chemists study quantum mechanics primarily in order to understand electronic structure. Various approximations to the multi-electronic wave function, and procedures to obtain the wave function numerically, are at the heart of computational chemistry courses. As a consequence, however, the conceptual use of quantum mechanics for a broad range of material properties, for fast motion or in spectroscopic observations, tends to be less developed. Here the current lecture series sets in.
We treat typical problems which are encountered in molecular spectroscopy, reactivity, or surface science. Each case is visualized as much as possible using characteristic parameters, and experimental observations are described. Ideally the lectures are given in a computer pool where students can write and run small model calculations by themselves, with help provided directly.
At first, we calculate the motion of the particle (atom, electron) in one dimension classically. Basic concepts like phase space, Hamiltonian, Newton´s equations, ensemble, and trajectory become familiar in this way. The effect of small external random forces, like collisions with solvent molecules, on a trajectory is mimicked, giving rise to ideas like coherence and dephasing. The motion of a classical probability distribution, or wave, is handled best after an expansion in basis functions. We will practice such expansions and produce classical wave motion.
It is then a small step to simulate wave motion
quantum-mechanically, starting with any given spatial distribution. In this way the time-dependent Schrödinger
equation is introduced. Stationary solutions are found numerically; their use in
creating wave motion becomes almost natural. At this stage the concept of a
representation is developed, and different representations are compared.
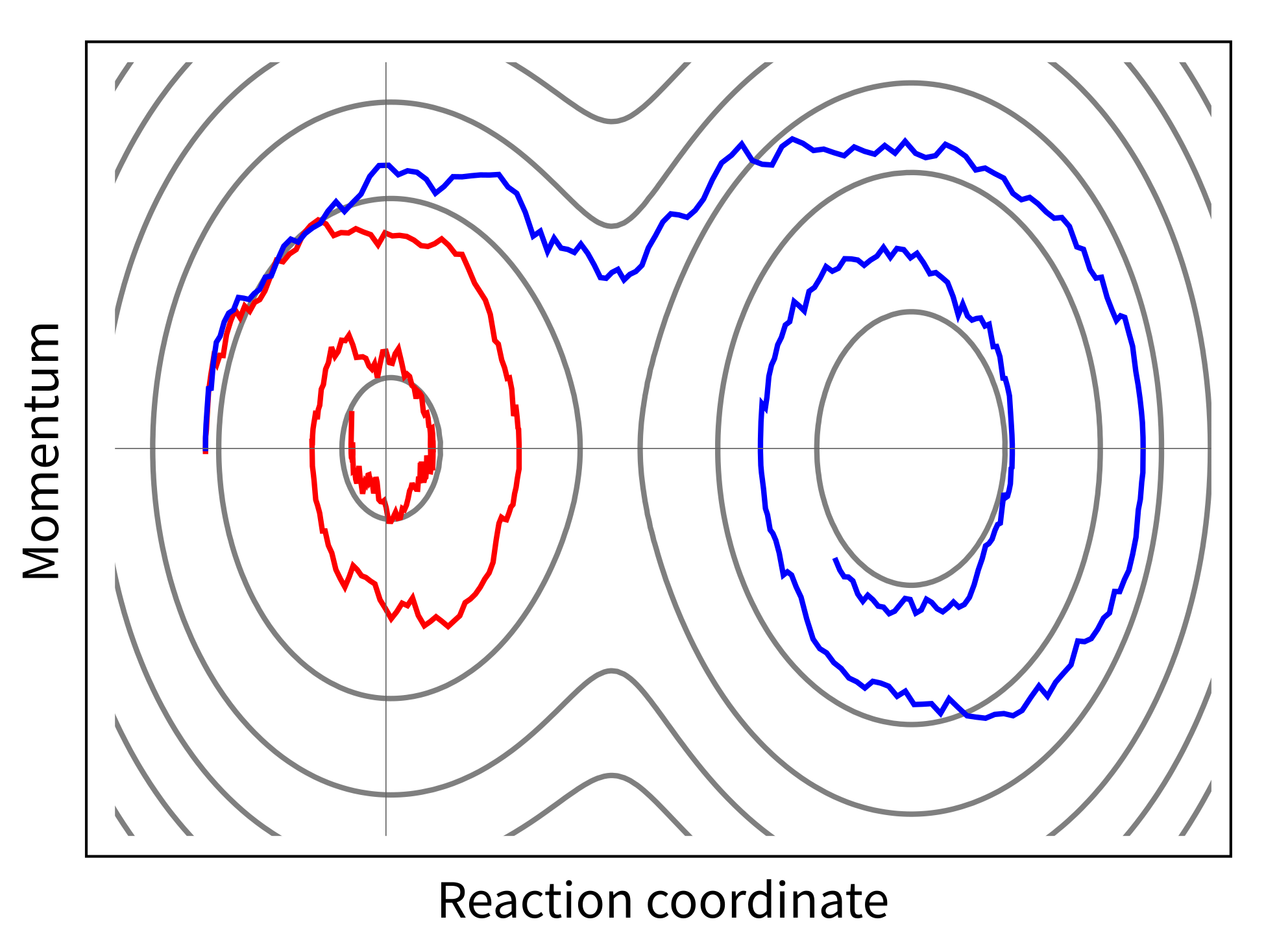
Several cases are treated practically and plotted: nuclear motion in an
anharmonic potential, or in a double minimum potential, and even a
“quantum-mechanical crash test” of a microscopic car-like distribution(q) that
is driven by a ramped potential against a stepped barrier.
Each chapter is equivalent to a 45-minute lecture plus 2 hours of practical work. In the lecture, the theory is developed and explained. The necessary mathematics is presented primarily in figures, as its structure can be highlighted by placements, colors, arrows, drawings etc. (copies of the sketches will be provided).
In the practical part, the example cases are treated numerically. For this we use Mathematica where analytical and numerical treatments can be mixed seamlessly. No prior knowledge of programming is required. During the practical part, the lecturers are available to assist the students. The time is dedicated to explore the concepts by playing with them.
- Course owner: Samuel Palato